計算機シミュレーションによる超低磁場MRIの原理 その2
磁化分布画像の再構成の原理
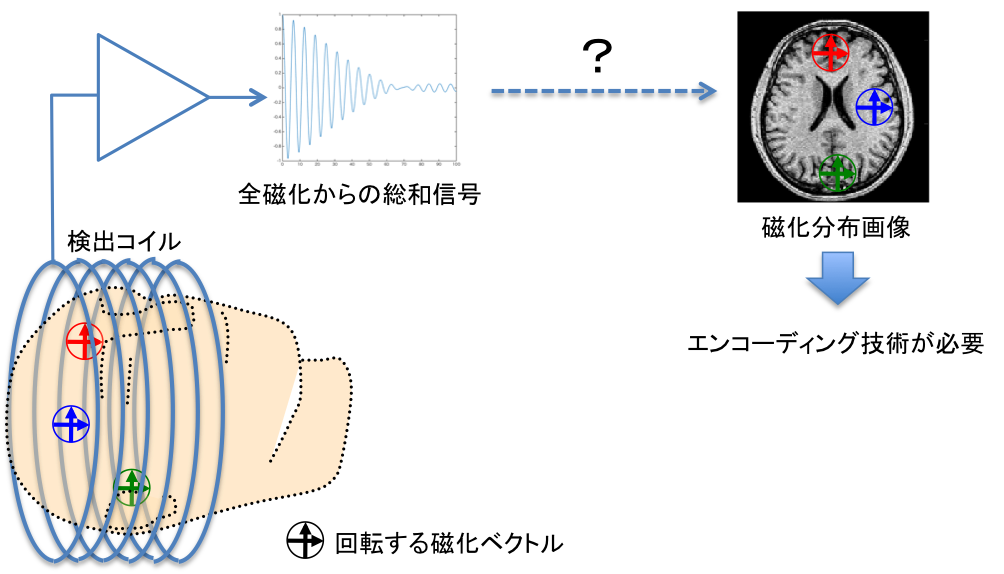
通常のMRIでは磁気共鳴信号検出は一つのセンサ(コイル)によって行われる。これは対象物全体からの総和信号であり、そのままでは磁化分布画像は得られない。そこで周波数や位相エンコーディングという手法を用いて磁化分布の位置情報を得る。
周波数エンコーディング
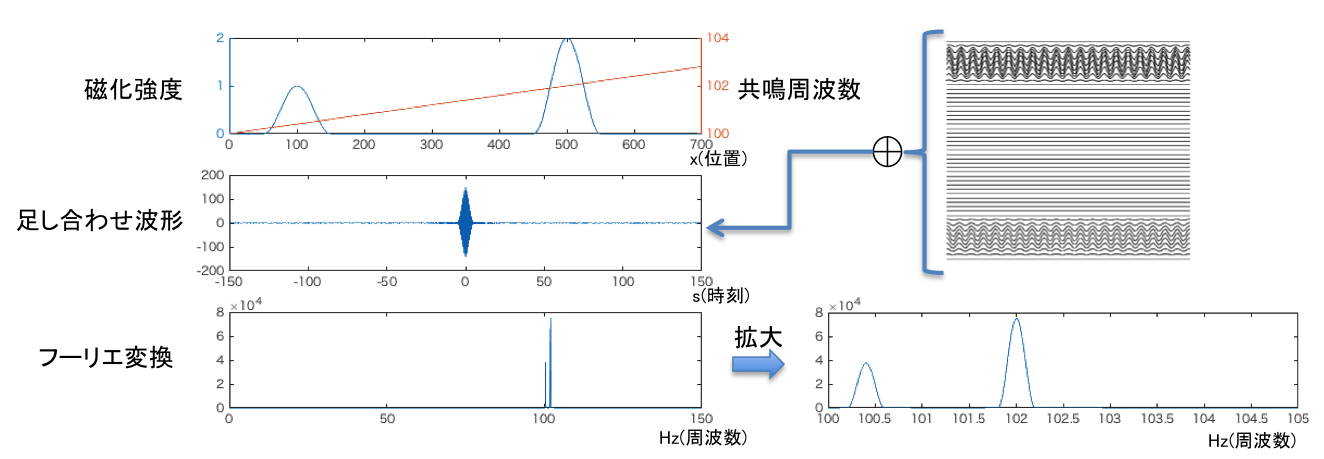
周波数エンコーディングは位置によって異なる磁場強度(傾斜磁場)を用いることによって、位置情報が共鳴周波数の違いによって表現されることを利用するものである。簡単な例として、一次元上の磁化分布を用いてシミュレーションを行った。下図のように1次元上に磁化分布している場合、共鳴周波数はx=0からx=700でf=100〜103に変化するものとする。たとえば、x=100では磁化強度は1で共鳴周波数は約100.4Hz、x=500ではに磁化強度は2で共鳴周波数は約102Hzである。各点における磁化強度を振幅とした共鳴信号を足しあわせたものを2段目に示す。サンプリング周波数は300Hzである。磁場の不均一によるFIDの減衰と同じ原理で、波形は時間と共に減衰する。この波形をフーリエ変換したものを3段目に示す。100Hz付近に2本のピークが立っている。この部分を拡大すると磁化分布の形状と一致していることが分かる。この場合、0-100Hzの部分は磁化分布の再構成には不要である。実際にはデータ間引き等を行ってこの部分を削除している。
位相エンコーディング
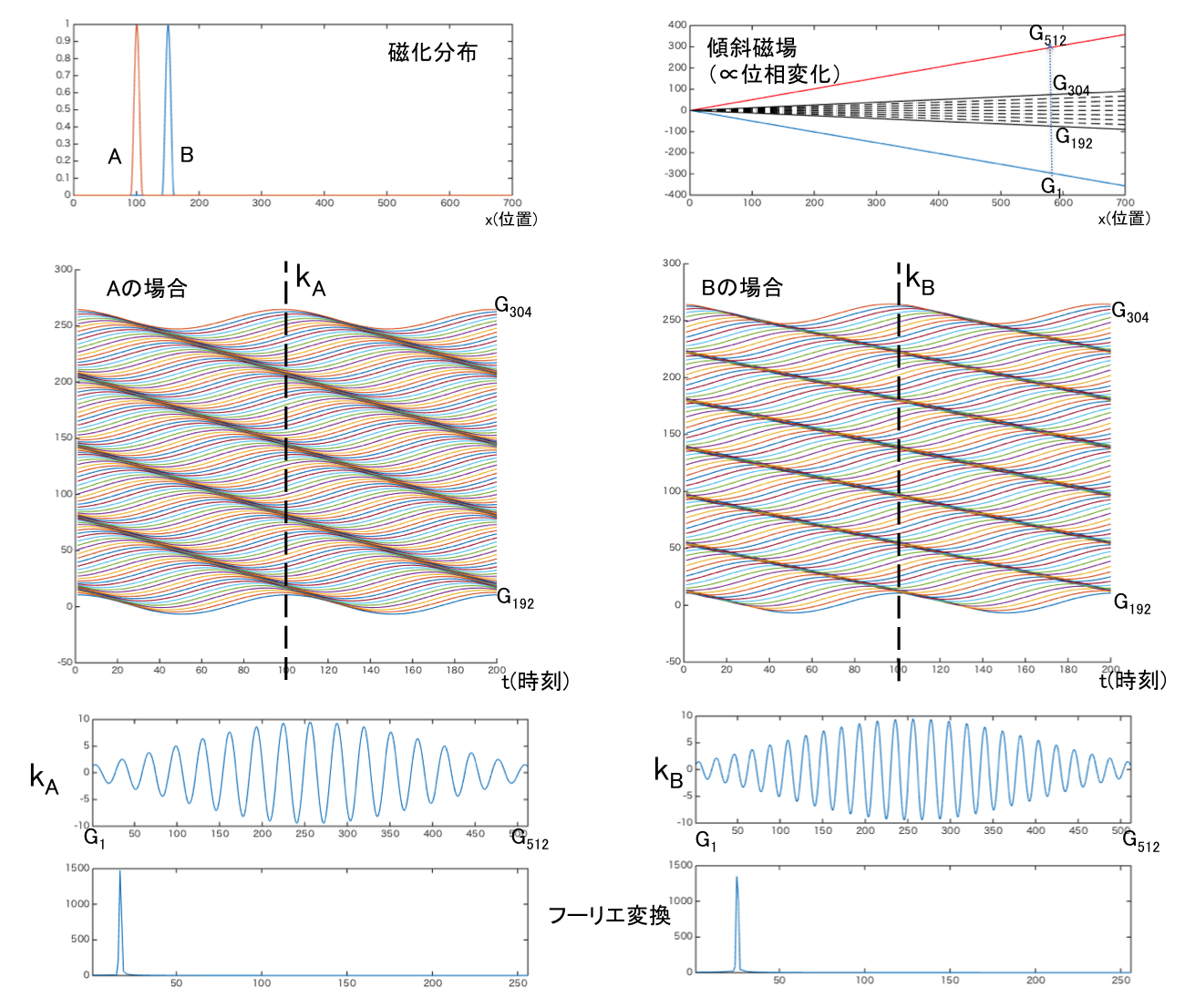
周波数エンコーディングと比較すると、位相エンコーディングは理解するのが少し難しい。信号には周波数の他に位相というパラメータがある。cos(2πf*t+θ)のθの部分である。このθを位置によって変化させることを位相エンコーディングと言う。その方法は傾斜磁場を一定時間加えることにより行う。周波数エンコーディングは傾斜磁場をかけている時にデータ収録するが、位相エンコーディングはデータ収録の前に傾斜磁場をかける点が異なる。位相の違いを知るには1回の計測だけでは分からないので、傾斜の異なる傾斜磁場を複数回かけてそのの波形の変化を指標とする。G1からG512までの傾斜磁場を掛けたときのA点とB点での計測波形を比較する。A点よりB点の方が位相の変化が大きいので、波形を横に並べた場合右斜めに見える縞の間隔が小さくなっている。これを時刻方向に対し垂直方向で見た場合、B点の方が早い周波数の波となる。これをフーリエ変換するとそのピーク位置がA点およびB点の位置に対応している。
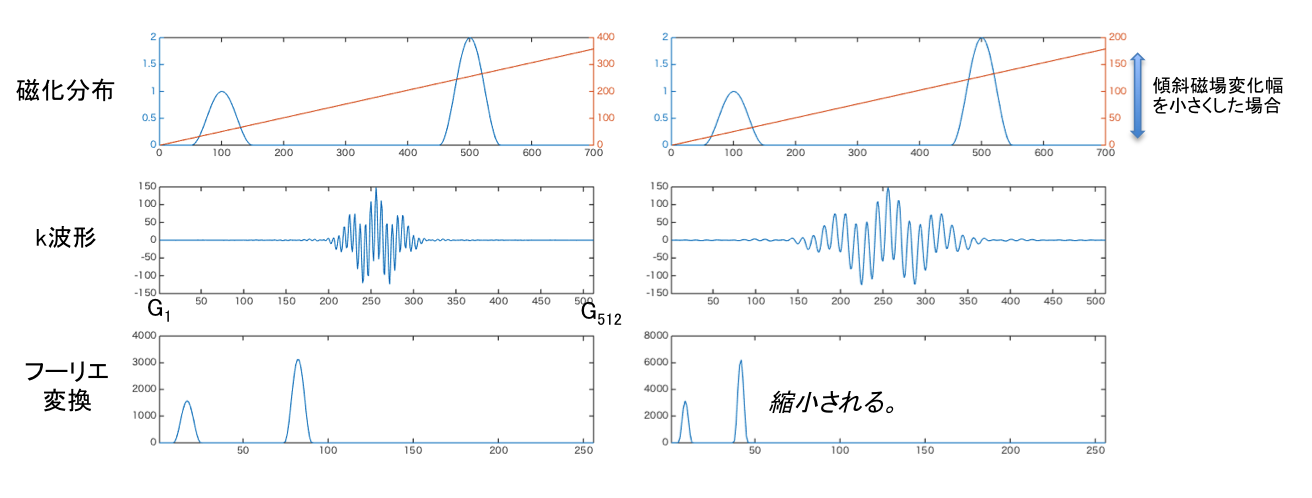
周波数エンコーディングの例と同じように2つのピークを有する磁化分布に適用した場合を下図に示す。
二次元分布の再構成
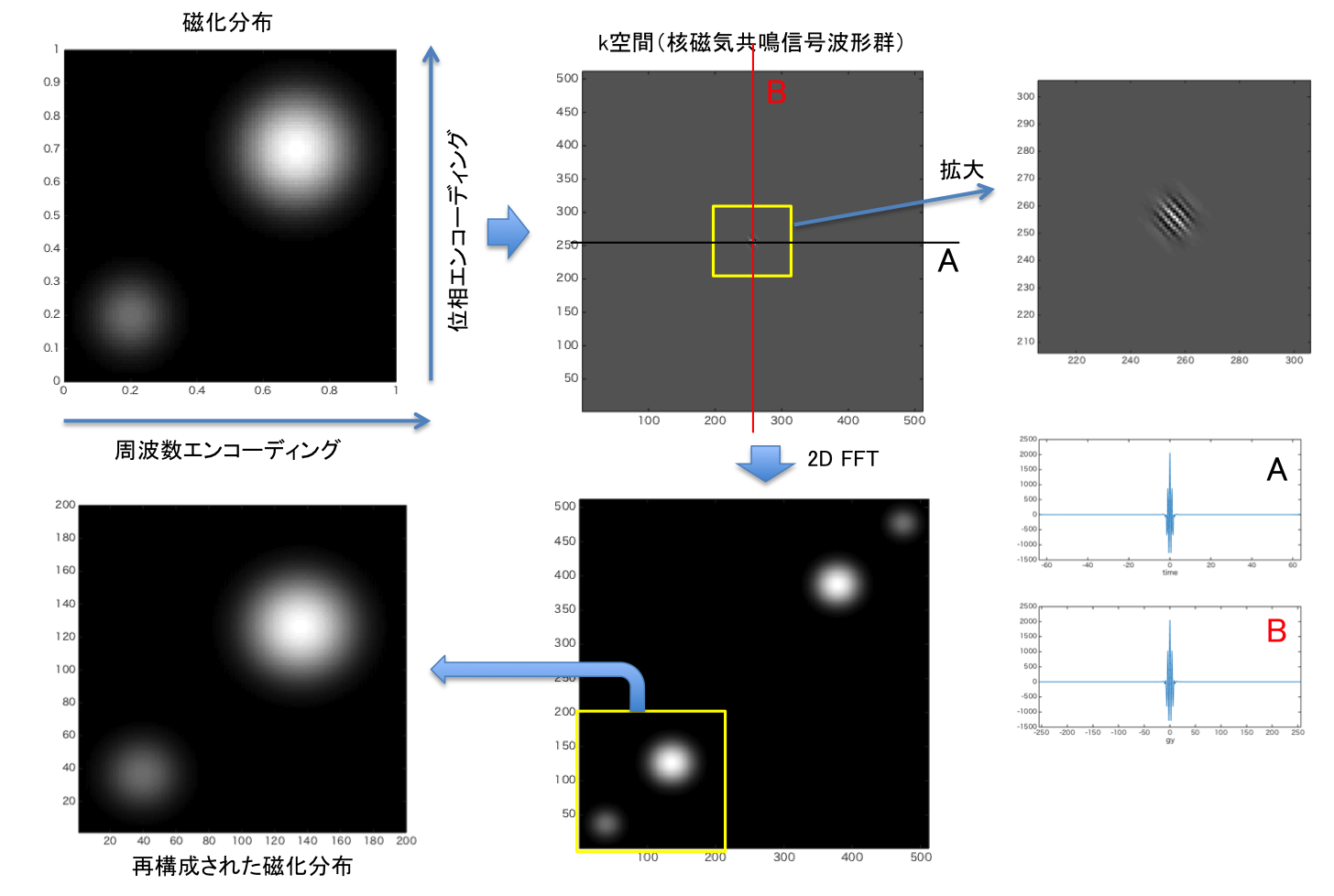
二次元の磁化分布を再構成するためには、周波数エンコーディングと位相エンコーディングを組み合わせて行う。下図にその例を示す。横方向に周波数エンコーング、縦方向に位相エンコーディングを行った。その波形群をk空間という。この例では周波数エンコーディングに512点、位相エンコーディングに512点を用いている。このk空間を2次元フーリエ変換すると磁化分布の再構成画像が得られる。実数波形を用いているので負の周波数領域にも再構成画像が現れている。なお、再構成画像の大きさや縦横比などはサンプリング周波数や傾斜磁場等によって変化する。これについては別途検討する予定。
つづく
