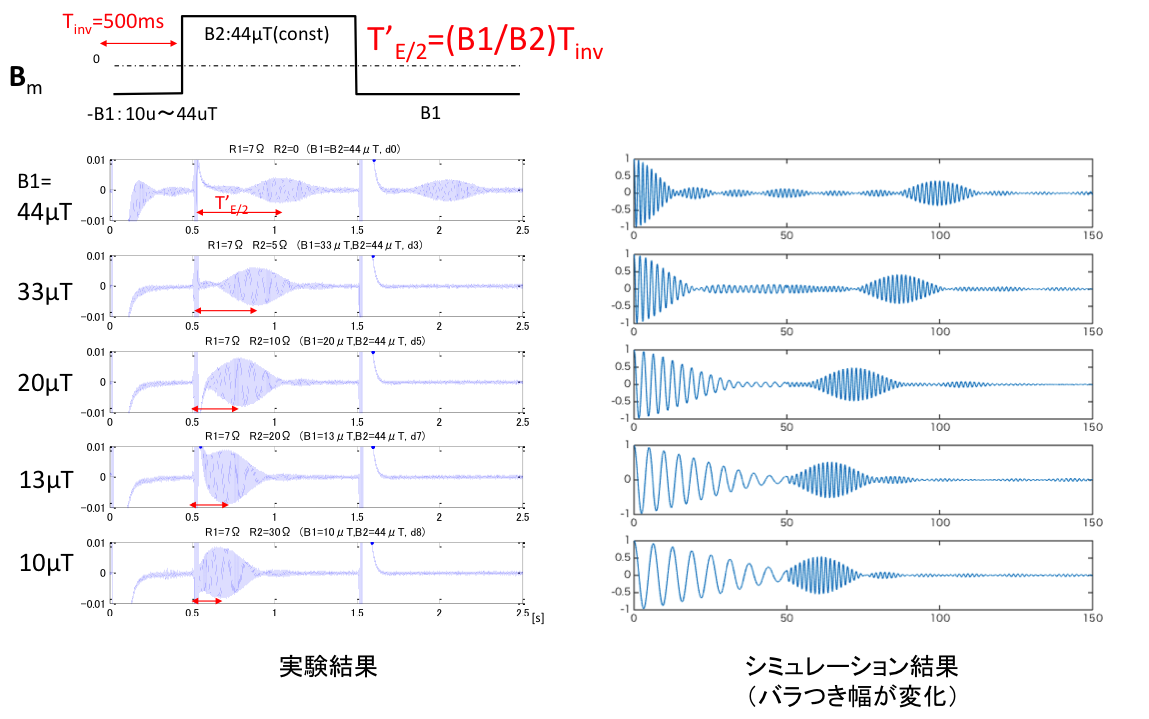
計算機シミュレーションによる超低磁場MRIの原理
エネルギー準位モデルと磁化ベクトルモデルによるスピンの記述
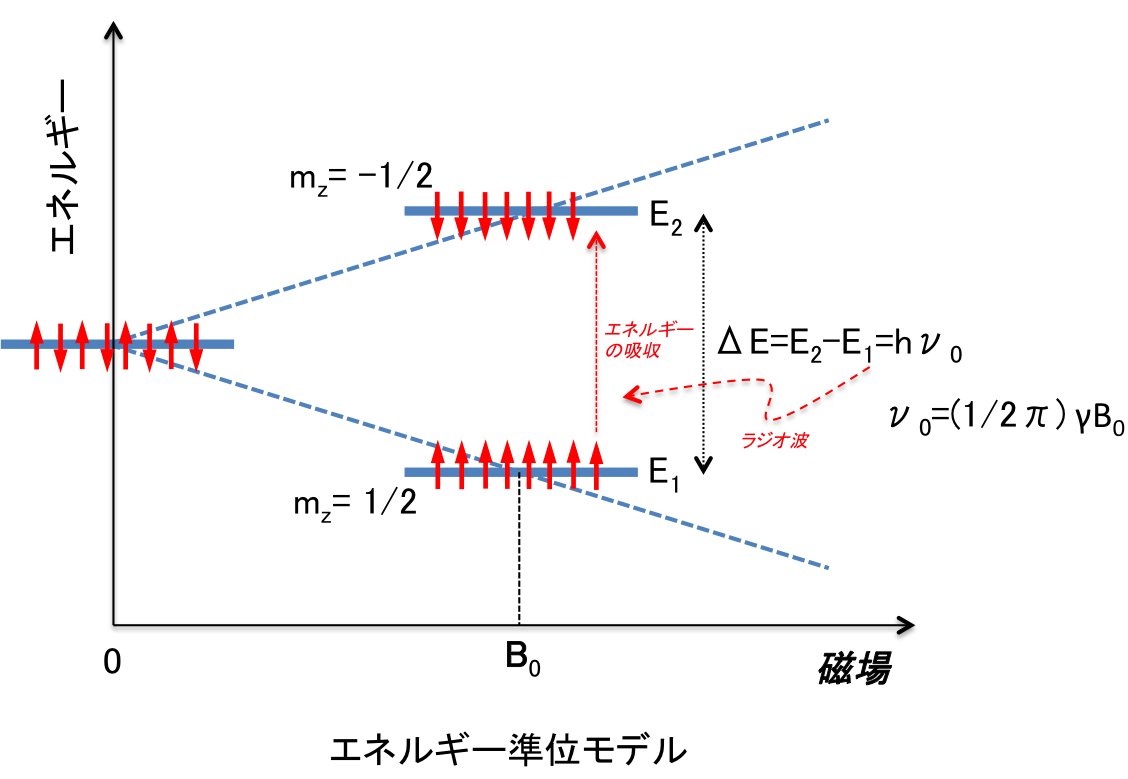
核磁気共鳴現象を記述するモデルにはエネルギー準位モデルと磁化ベクトルモデルがある。エネルギー準位モデルは量子論に基づくもので、詳しくは他の専門書等を参照していただきたいが、ここでは私の理解した範囲で概要を示す(間違っていたらごめんなさい。)スピンはスピン量子数と呼ばれる物理量を有し、それは1/2,1,3/2等の不連続な値をとる。水素原子(プロトン)のスピン量子数は1/2で、外部磁場が存在する場合、+1/2と-1/2の二つのエネルギー状態に分かれる。これをゼーマン分裂と呼び、そのエネルギー差は外部磁場の大きさに比例する。そのエネルギー差に相当する電磁波を照射すると、下の準位のスピンはエネルギーを吸収して上の準位に行き、上にいるスピンはエネルギー放出して下の準位に遷移する。これが同時に起こることから共鳴と言われる。共鳴を起こす電磁波の周波数はエネルギー差すなわち外部磁場の大きさに比例する。下→上、上→下の遷移確率は等しいので、下の準位のスピン数がわずかだけ多い分、吸収が放出を上回る。照射電磁波の周波数を連続的に変化させていき、受信信号が急に減少する周波数が共鳴を起こしている周波数となる。
一方、磁化ベクトルモデルは個々のスピンを小さな棒磁石と見なし、その集団としての巨視的磁化の挙動を古典物理(電磁気学)を用いて記述するものである。エネルギー準位モデルは物質の成分分析(NMR分光法)や精密な核磁気共鳴現象を考察するのに有効であり、磁化ベクトルモデルは核磁気共鳴画像(MRI)で用いられる縦磁化・横磁化等を考える際に有効と言われている。以下においては磁化ベクトルモデルを用いてシミュレーションを行い、超低磁場MRIに関する検討を行う。
静磁場不均一による横磁化減衰のシミュレーション
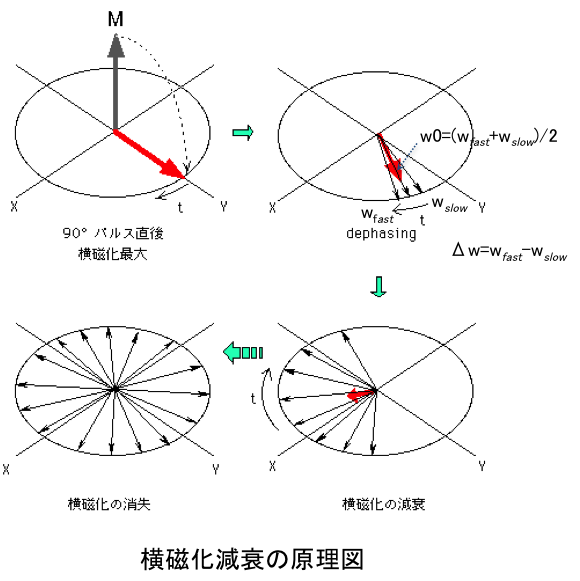
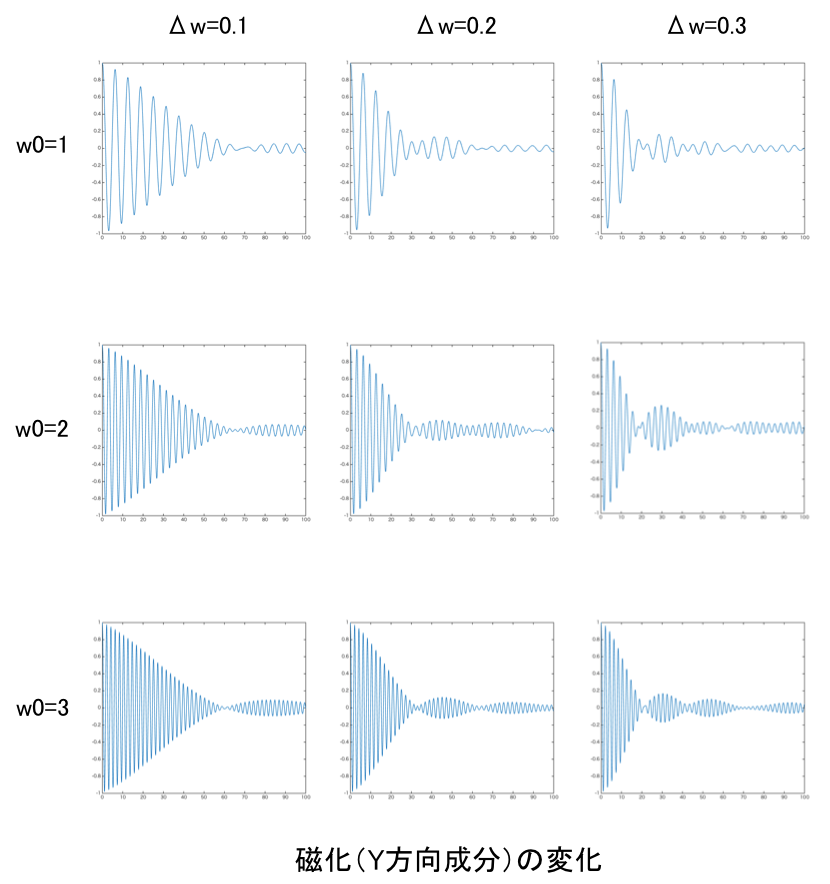
90度パルスによって直交面に倒された磁化は静磁場の不均一により個々のスピンの回転速度にズレが生じ、横磁化が時間とともに減衰する。この現象を100個の回転するベクトルを使ってシミュレートしてみた。平均回転速度w0を1[radian/s]とし、個々のベクトルの回転速度はズレ幅Δwにランダムに分布するものとする。青丸が個々のスピンの先端、赤棒が平均化された磁化ベクトルを示す。回転速度のズレ幅が静磁場不均一幅に対応する。図に示すように、平均磁化の減衰速度はΔwの大きさで決まり、w0の大きさには関係しない、すなわち、減衰の速さは静磁場不均一の絶対値で決まり、静磁場の大きさには関係しないようだ。ただし、ヘルムホルツコイルで静磁場を作る場合、静磁場の大きさ(ヘルムホルツコイルに流す電流)に比例して磁場不均一幅も大きくなるので、結果、静磁場を大きくするするほど横磁化の減衰は早くなるものと予測される。
スピンエコーのシミュレーション
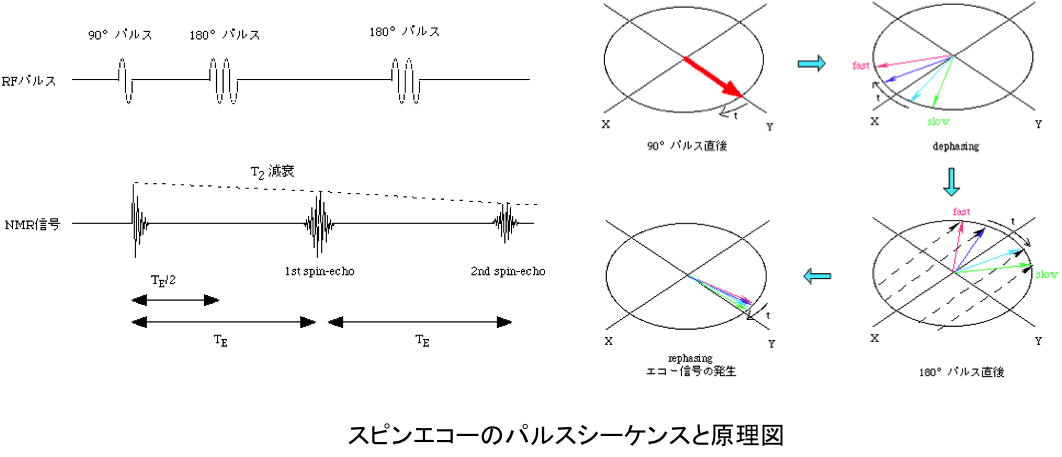
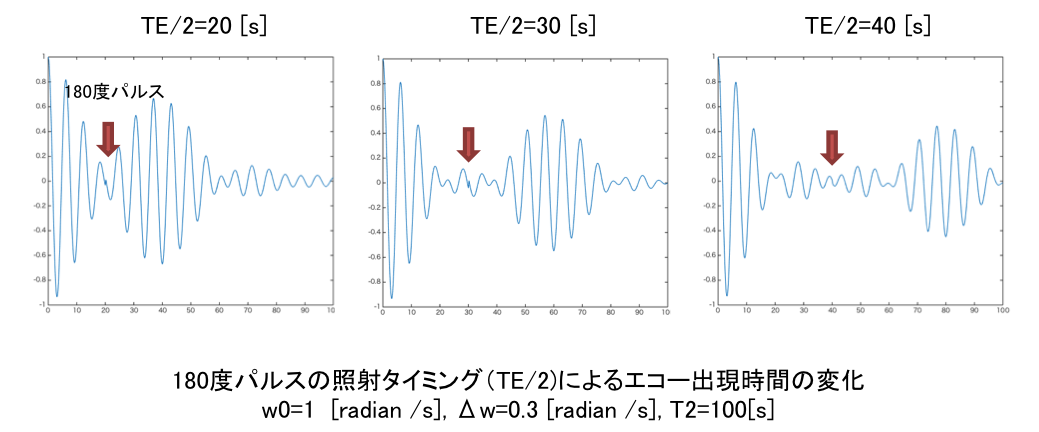
RFパルスによるスピンエコーは90度パルスを照射後、ある一定時間間隔で180度パルスを照射するもので、分散した個々のスピンが180度パルスにより再びそろうことで横磁化が大きくなる現象(エコーの出現)である。動画の赤丸が回転速度の一番速いスピン、黒丸が一番遅いスピンを示している。途中で速いスピンと遅いスピンの位置関係が逆転し、速いスピンが再び遅いスピンを追い抜く時に大きな磁化となる様子がわかる。180度パルスのタイミングを変えるとエコーが出現する時間も変化する。
静磁場の反転によるスピンエコー
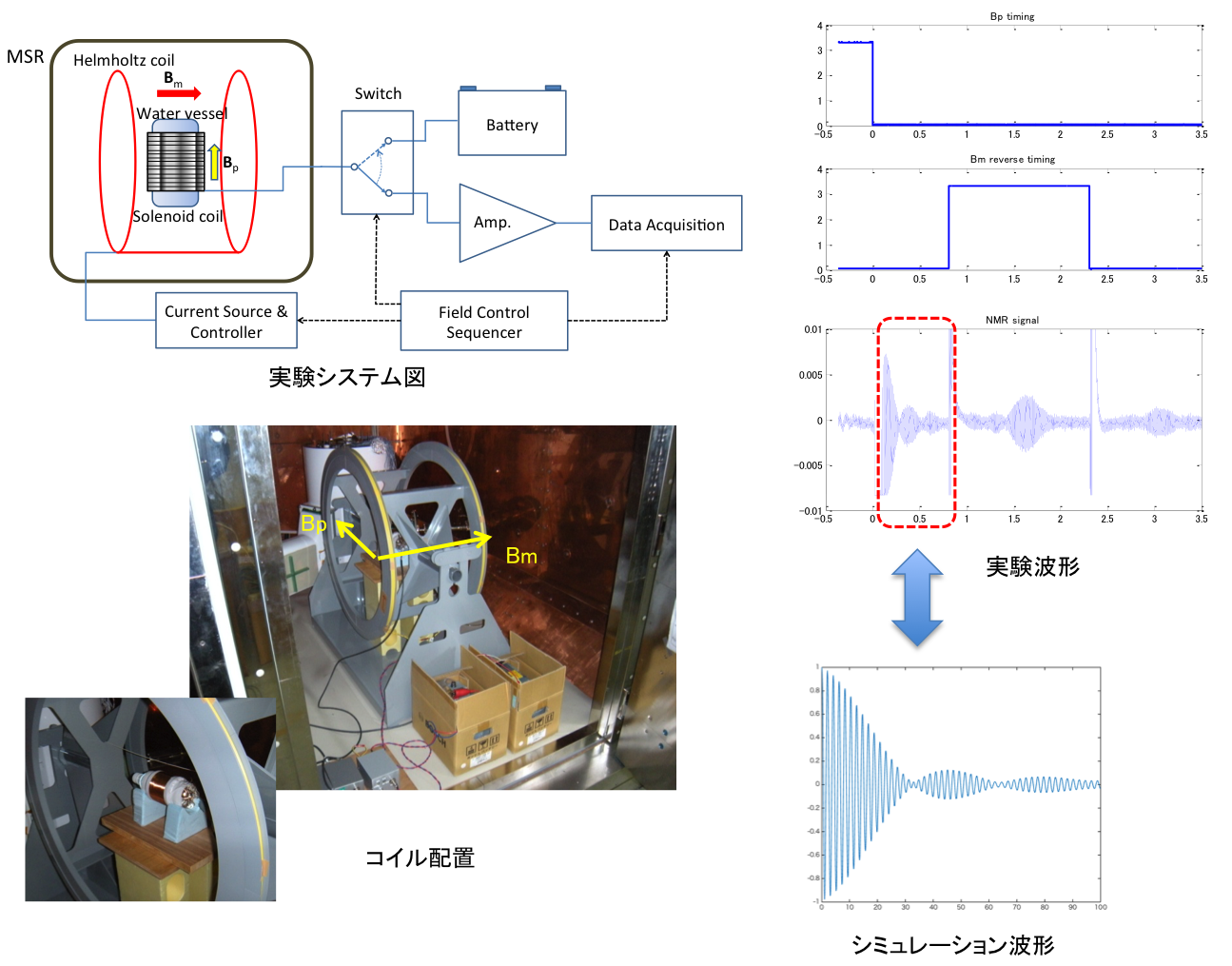
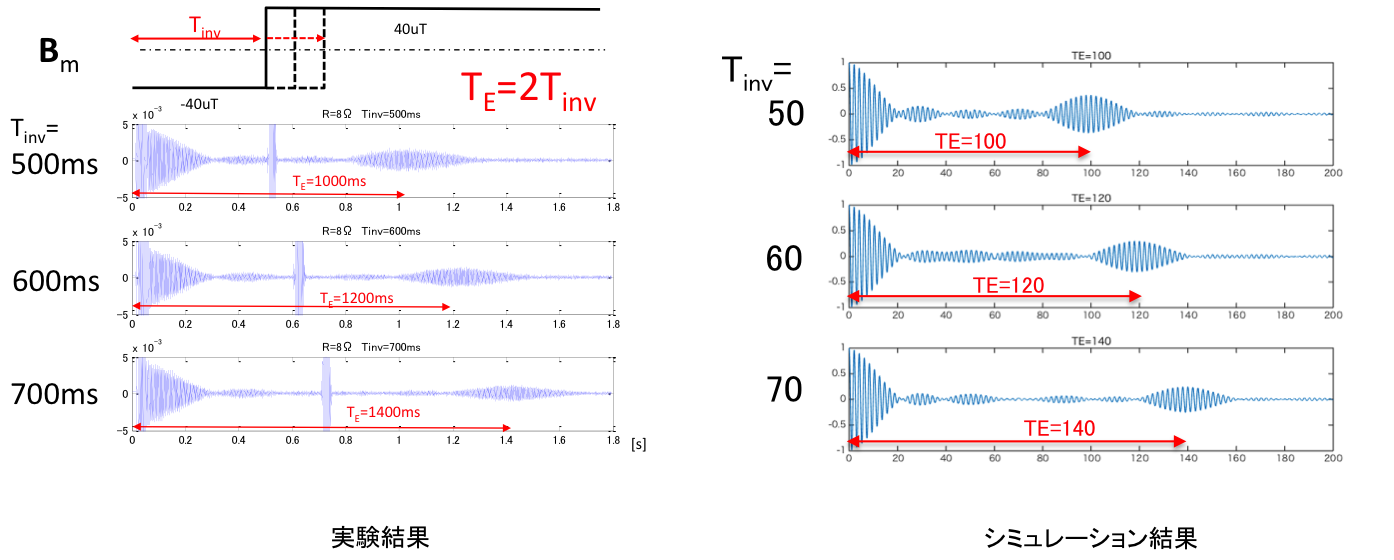
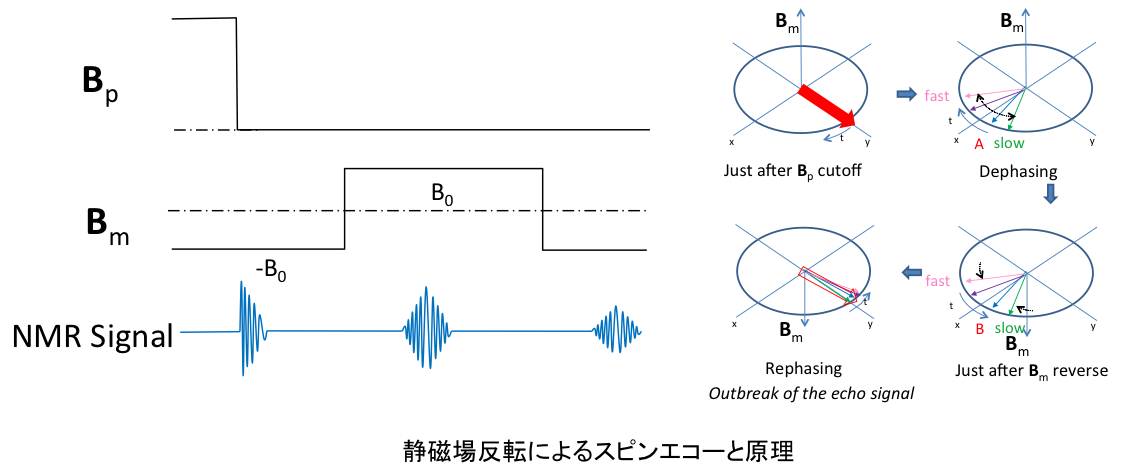
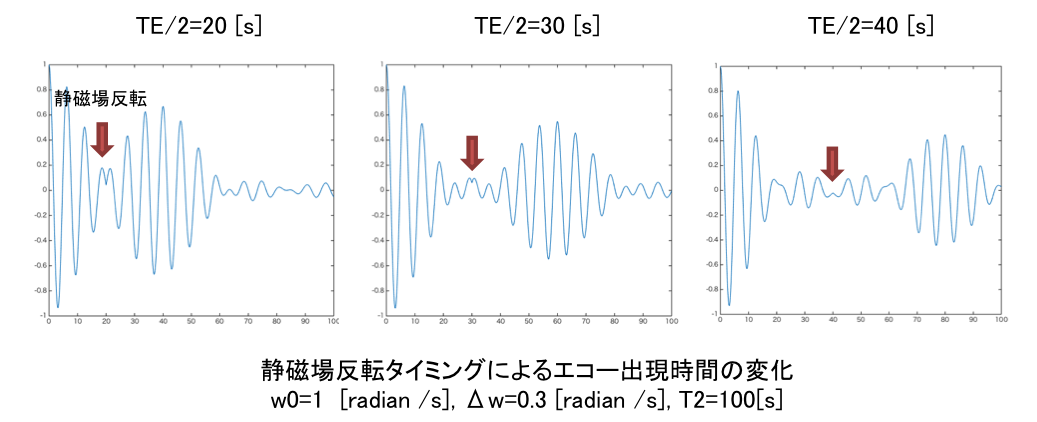
超低磁場MRIで良く用いられる方法で、RFパルスの代わりに静磁場を反転させることでスピンエコーを実現することができる。分極磁場遮断後、時間とともにスピンが分散して行くが、静磁場を反転すると回転する向きが反対になり、早く進んでいたスピンが後ろに、遅く進んでいたスピンが前になる。ヘルムホルツコイルで静磁場を作る場合、コイルに流す電流を反対にすれば良く、磁場の絶対値は同じである。したがって、各スピンの速度の絶対値は変化しないので、後ろになった速度の速いスピンは前になった遅いスピンをいずれ追い抜くことになる。このときに全体としての横磁化が大きなる、つまりエコーが発生する。先の動画と同じように赤丸が一番速いスピン、黒丸が一番遅いスピンを示しており、途中で回る向きが反転している。RFパルスのスピンエコーと同じように、磁場を反転するタイミングを変えるとエコーが出現するタイミングも変化する。
非対称スピンエコー
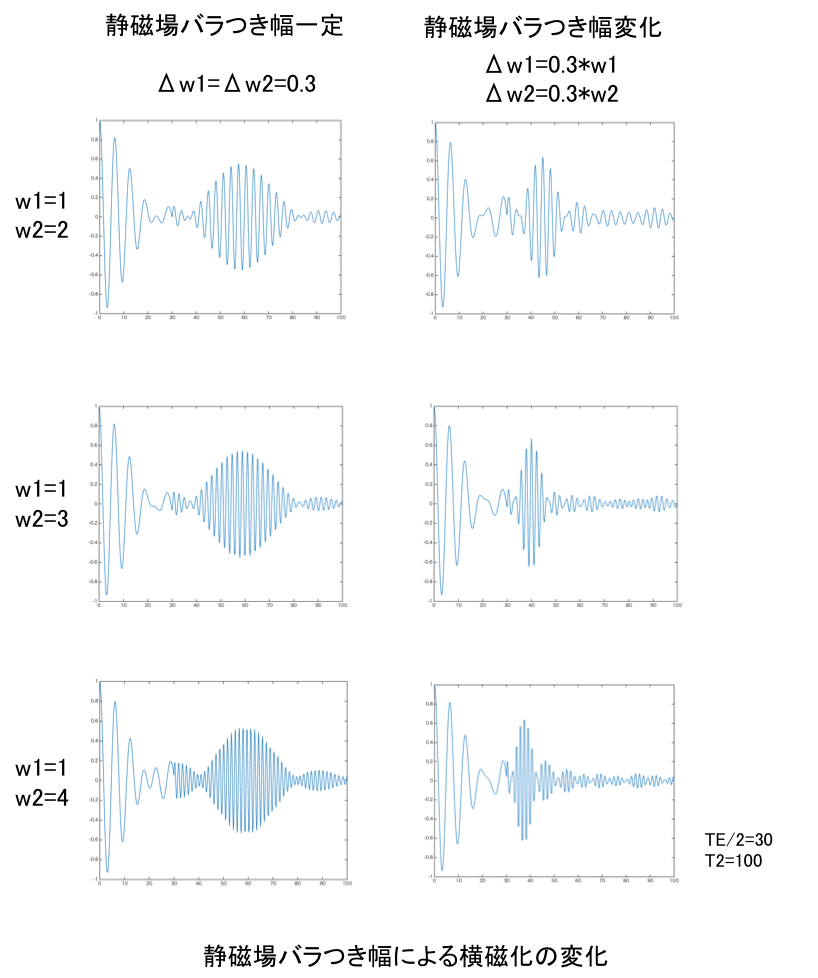
静磁場反転によるスピンエコーにおいて反転させる静磁場の絶対値は同じとしたが、両者が違っていてもエコーは発生する。ここではこれを非対称スピンエコーと呼び、そのシミュレーションを行った。動画は初めの静磁場に対して3倍の大きさの静磁場を反対向きにかけたときを示しており、途中で回転速度が速くなっている。各スピンの回転速度のばらつき幅を2種類検討し、一つは一定、もう一つは静磁場の大きさに比例してばらつき幅も大きくなるとした。一定の場合は、エコーが出現するタイミングは同じである。ばらつき幅が変化する場合には、静磁場が大きくなるにしたがってエコー出現時間が短縮する。実際にヘルムホルツコイルで磁場反転を行う場合は後者になると思われる。