コヒーレンス関数を用いた聴覚反応の評価

聴覚誘発脳磁場計測

MEGから得られる脳磁場信号は、外来ノイズに加え自発性脳磁場やその他の刺激誘発脳磁場などの重ね合わせ波形であり、加算平均法なしでは目的信号を単独波形として取り出すことは困難である。そのため聴覚誘発磁場計測においては、一定の幅を持ったバースト音や音声（単音・単語）を繰り返し提示しその時に得られる脳磁場データを加算平均して反応波形を抽出する。

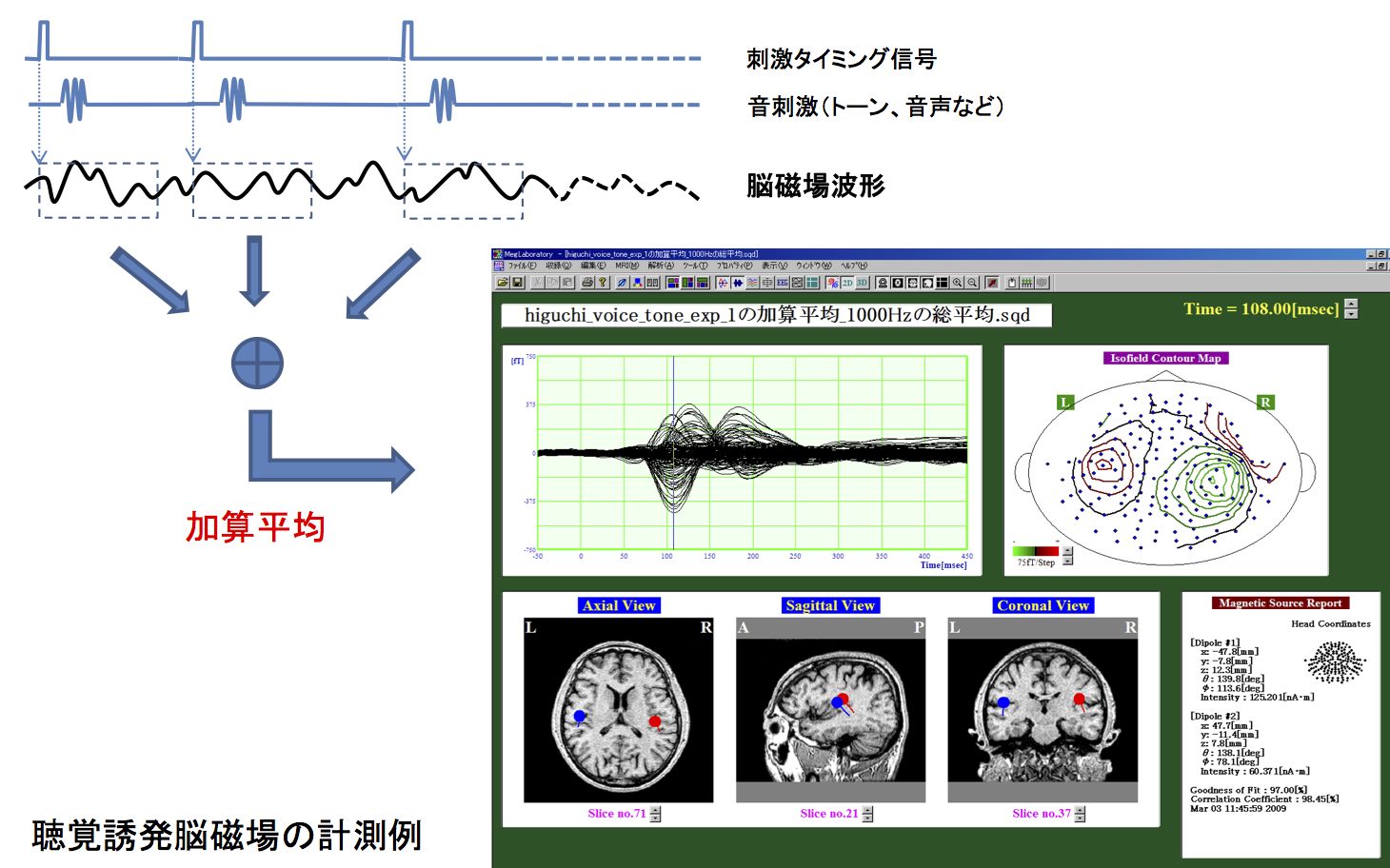
しかし、この方法では音楽や人の話声などに対する全体的な脳反応を知ることはなかなか難しい。そこで、このような一連の音に対する反応を評価するする方法として、音のエンベロープとのコヒーレンス関数を用いた評価方法を考案した。本手法は聴覚誘発磁場波形そのものを知るための方法ではなく、提示している音に対して観測された脳磁場波形がどの程度相関性があるのかを評価するものである。

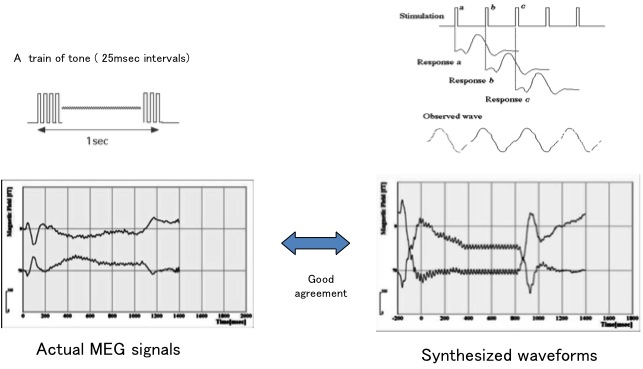
音が連続して続いたときの聴覚誘発磁場波形

クリック音や短い幅のトーンなどを繰り返し提示し、そのときの脳磁場信号を加算平均すると先の図に示したような波形で、線形システムにおけるインパルス応答のような形状をしている。これより連続音に対する脳磁場波形は、この単発音に対する反応波形を連続音の強弱で重みを付けながら時間をずらしてし足し合わせた波形（畳み込み波形）となることが予測される。実際にクリック音に対する反応波形を用いてクリック音が連続した場合の反応波形を合成した結果、実際の計測波形とある程度一致することが確認された。したがって、連続音に対する脳磁場波形は音の強弱波形（エンベーロープ）と相関性を有しており、これをコヒーレンス関数を用いて評価する。

コヒーレンス関数

コヒーレンス関数は２つの信号の因果関係を調べる際に用いる評価量で、以下の式で表現される。

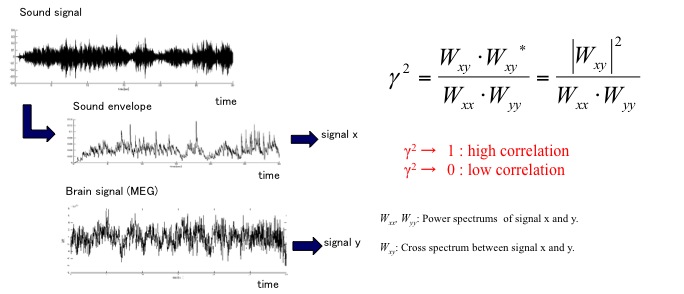
ここでは、Wxxは音信号のエンベロープ波形のパワースペクトル、Wyyは脳信号のパワースペクトル、Wxyは音信号のエンベロープ波形と脳信号とのクロススペクトルとなる。この関数は0から1の間の値をとり、0に近い場合両者の相関性は低く、また、1に近い場合は非常に相関性が高いことを意味する。

確認実験

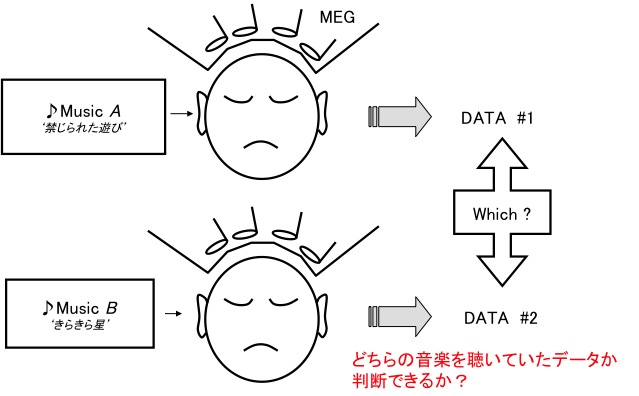
2種類の音楽（禁じられた遊び、きらきら星）をそれぞれを単独で聴いた場合の脳磁場を計測し、各記録データに対してどちらの音楽を聞いていたかを判別することができるか検証した。音楽はそれぞれ1分間の長さで、磁気シールドルーム内でイヤチューブを用いて被験者に提示した。記録したMEGデータはオフラインフィルタ処理、ダウンサンプリング処理、空間フィルタ処理等の前処理を行い、コヒーレンス(関数)値を計算した。

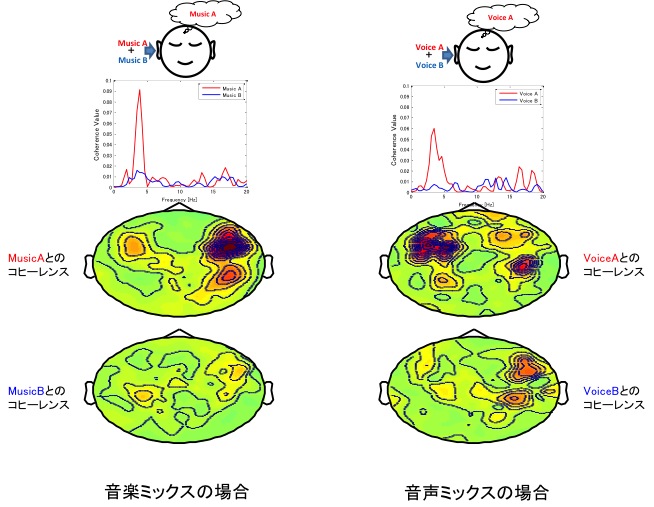
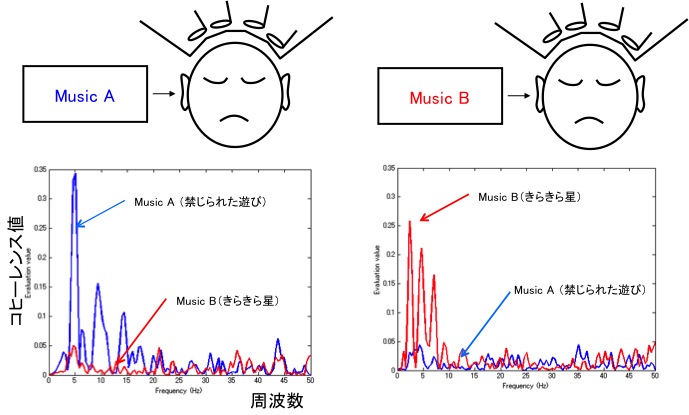
下図はそれぞれのコヒーレンス値をグラフ化したものである。比較のため提示していない方の音楽とのコヒーレンス値を重ね書きした。それぞれ聞いている音楽に対するコヒーレンス値が提示していない音楽よりも明らかに増加していることが示されている。つまり、計測されたMEGデータからどちらの音を聞いているかを判別できることを示している。

カクテルパーティー効果への応用

本手法を用いてカクテルパーティー効果に関する検討を行った。カクテルパーティー効果は選択的聴取のことで、雑音や複数の音声の中から特定の音声のみを聞き分けることを言う。実験は２つの音源をミックスした音を提示し、一方の音に注意している時のMEG信号を計測した。一回の計測で提示した音の長さは３分間で、磁気シールドルームの外からイヤチューブを用いて被験者の両耳に提示した（モノラル）。

下図はコヒーレンス関数の一例と2-6Hzのコヒーレンス値の和を全MEGセンサで算出し等高線表示したものである。注意している音に対するコヒーレンス値が増加する傾向が得られた。また音声(Voice)の場合、左半球のコヒーレンス値が大きくなる傾向がえられた。左半球のコヒーレンス値の増加ということは言語機能との関連性が示唆される。